Robust Parameter Design
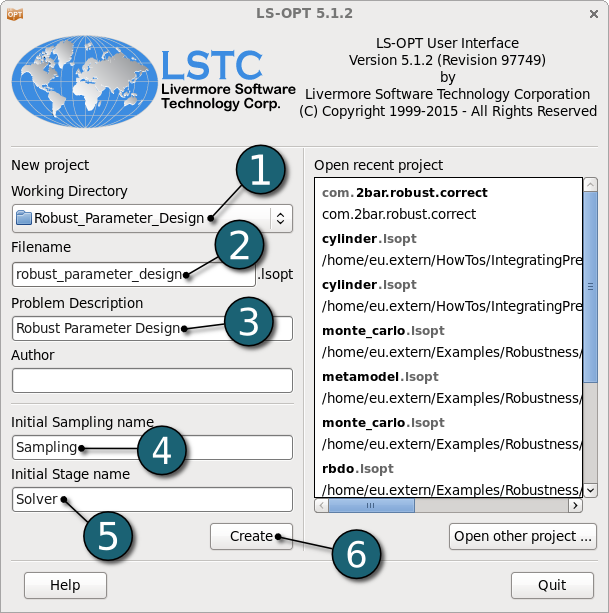
Working Directory and Extraction of necessary files
- Create a working directory in the desired location to keep the LS-OPT project file and input files, as well as the LS-OPT program output, e.g. Robust_Parameter_Design.
- Extract all the files required for this example from download section into the working directory.
Project Details
- Select the Working Directory of the LS-OPT project.
- Select a suitable name for the file under Filename (e.g. robust_parameter_design. The extension .lsopt is appended by LS-OPT.
- Description of the main task can e.g. be a suitable name for Problem Description ( in this case, Robust Parameter Design, optional) .
- Choose a suitable name under the Initial Sampling name (e.g. Sampling).
- Choose a suitable name under the Initial Stage name (e.g. Solver).
- Click on the Create button to initiate the formation of the input file.
- The main GUI window of LS-OPT opens.
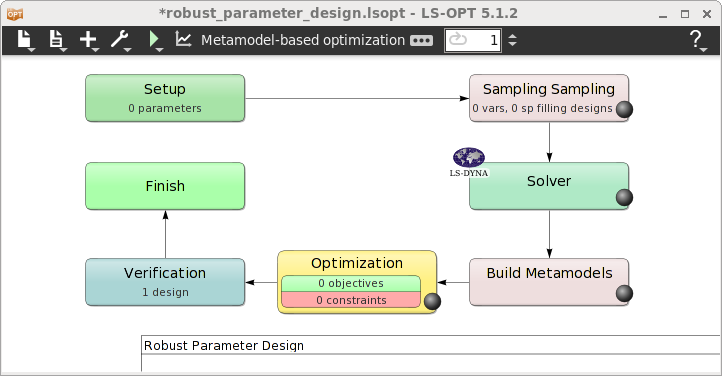
Home Screen Process Flowchart
- Click on the Show task settings icon to select the optimization task and strategy.
The Task Selection window shall then open.
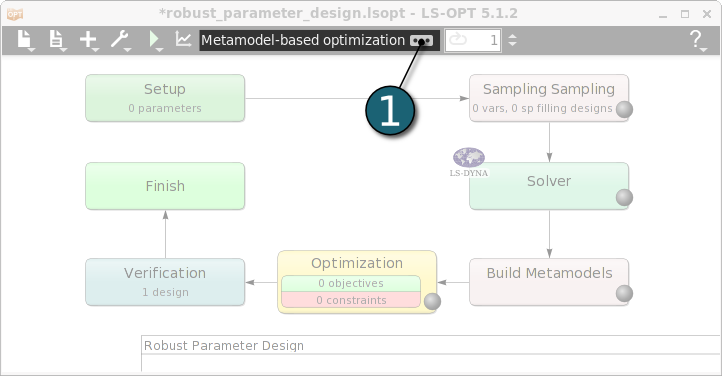
Define the Main Task
- Select RBDO/Robust Parameter Design for the Metamodel-based main task.
- Select Sequential with Domain Reduction (SRSM) as the Strategy for Metamodel-based Optimization.
- After the last full iteration Do verification run to execute a simulation using the predicted optimal parameter values.
- Click on the OK button to proceed.

- After defining the main optimization task the Home Screen Process Flowchart takes its shape accordingly.
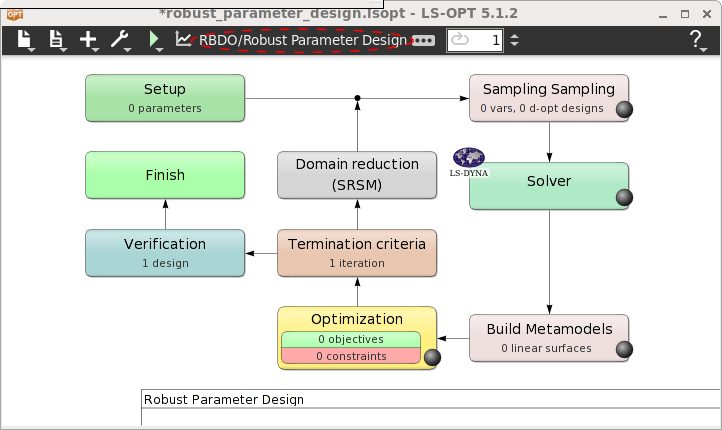
Home Screen Process Flowchart
- Double click on the Solver stage.
The Stage Solver dialog shall open.
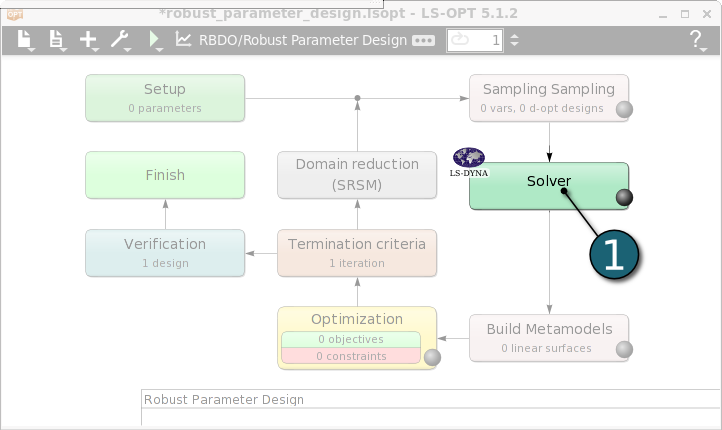
Define Stage Setup
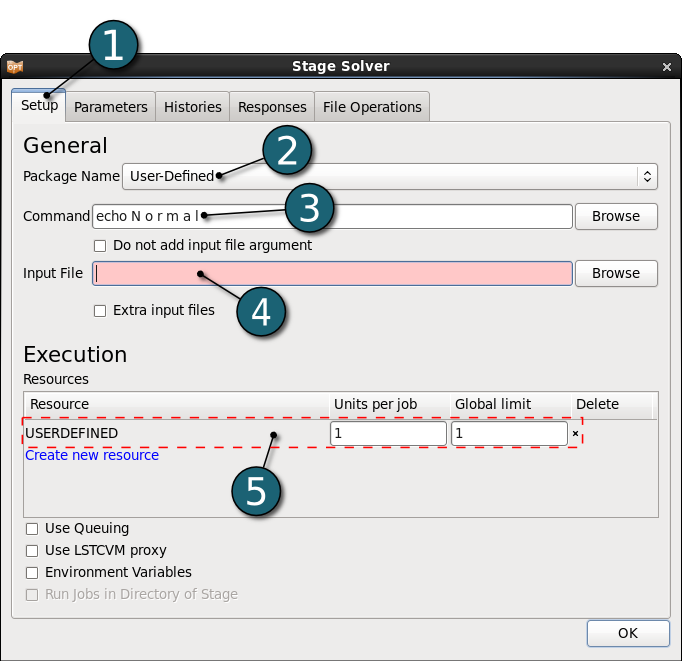
- Select Setup tab.
- Select User-Defined as Package Name.
- For Command type echo N o r m a l which signals LS-OPT a normal termination for the solver stage. Since this is an analytical example, the responses are directly defined directly as expressions depending on the parameter. Note that on Windows a batch script has to be used here.
- For the same reason, no input file is needed in this example. The analytical solution of the problem will simply be defined in the Responses below.
- For efficient usage of the computing power from the machine, choice on handling number of concurrent jobs can be made suitable in this section. For more details see FAQ resources.
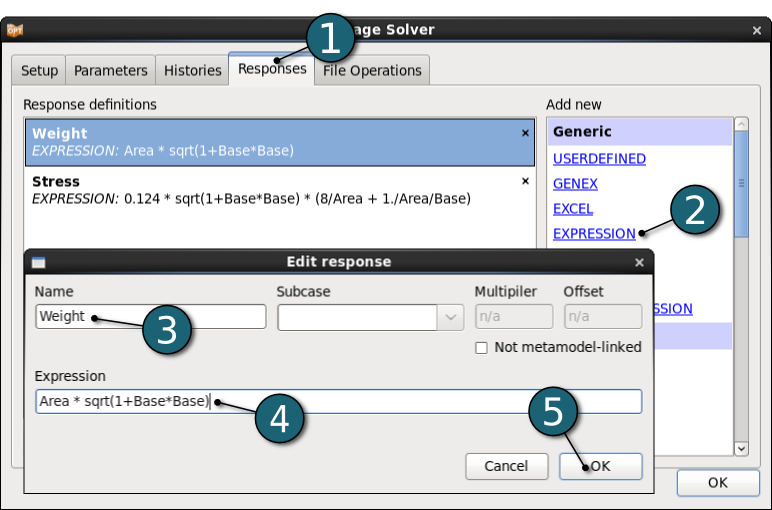
Define Responses
Define Weight
- Select Responses tab.
- Select EXPRESSION as a response type.
- Enter Weight as response Name.
- Enter the Expression
Area * sqrt(1+Base*Base)
to calculate the mass of the structure. - Click on the OK button to end the definition of the response Weight.
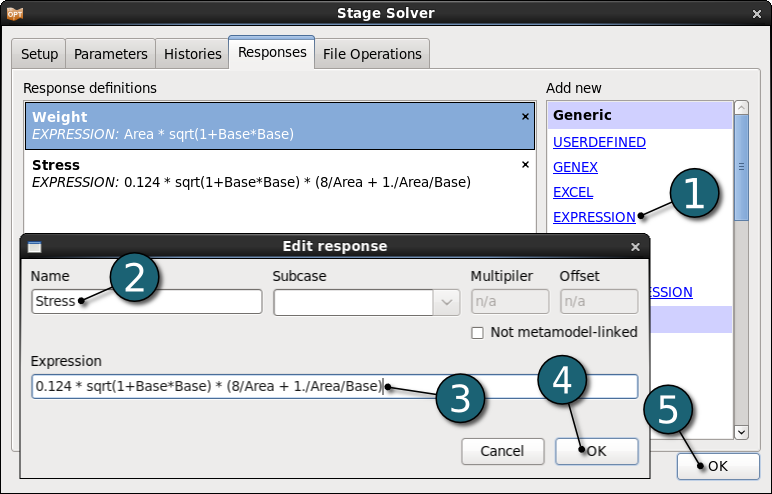
Define Stress
- Select EXPRESSION as a response type.
- Enter Stress as response Name.
- Enter the Expression
0.124 * sqrt(1+Base*Base)
* (8/Area + 1./Area/Base)
to calculate the stress in the structure. - Click on the OK button to end the definition of the response Stress.
- Click on the OK button to proceed.
Home Screen Process Flowchart
- Double click on the Setup box to define the design variables.
The Problem globel setup dialog shall open.
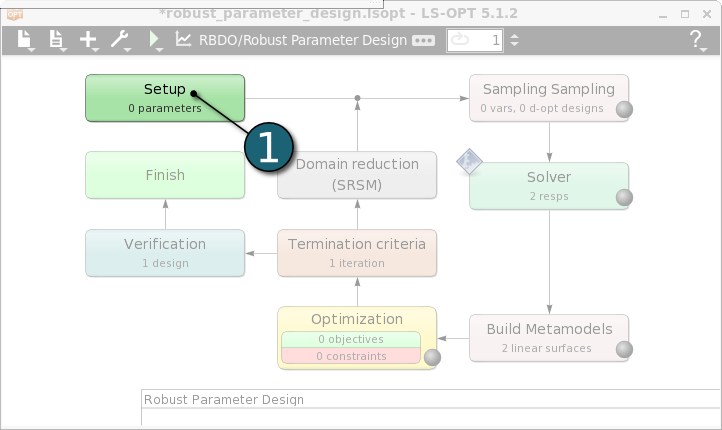
Define Parameters
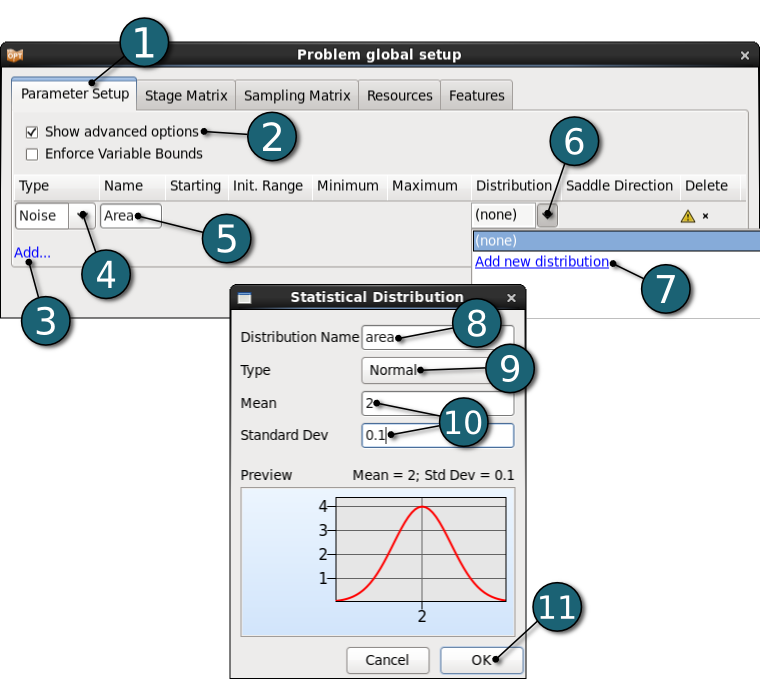
Define Area
- Select Parameter Setup tab.
- Click on the Add to define new parameter.
- Activate Show advanced options.
- Select Noise for the Type of the variable.
- Enter Area for the Name.
- Select the options for Distribution of the variable.
- Click on the Add new distribution.
- Enter area for Distribution Name.
- Select Normal as the Type of distribution.
- Enter 2 and 0.1 for the Mean and Standard deviation, respectively.
- Click on the OK button to define the distribution.
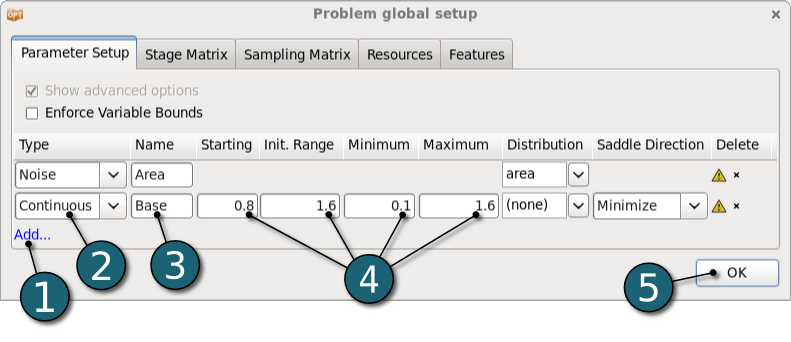
Define Base
- Click on the Add to define new parameter.
- Select Continuous for the Type of the variable.
- Enter Base for the Name.
- Enter 0.8, 1.6, 0.1 and 1.6 for Starting, Init. Range, Minimum and Maximum, respectively.
- Click on the OK button to proceed.
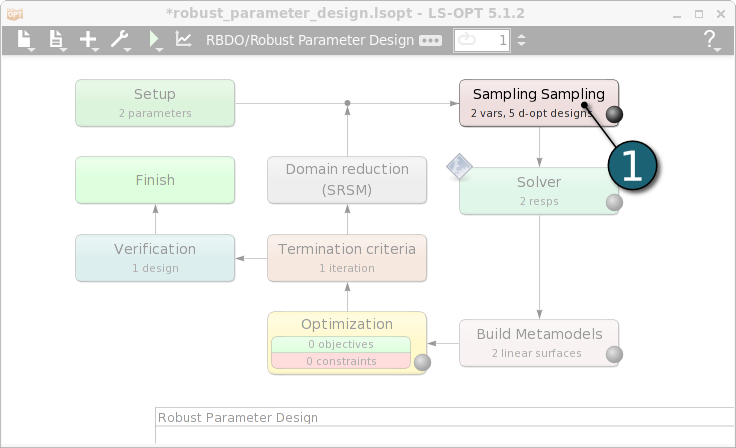
Home Screen Process Flowchart
- Double click on the Sampling box in order to define sampling settings.
A Sampling dialog shall open.
Define Metamodel Settings
- Select Metamodel Settings tab.
- Select Polynomial as a Metamodel type.
- Select Linear with interaction as the Order of the polynomial metamodel to get more accurate statistical results.
- Select D-Optimal as the Pointselection method.
- Use the default Number of Simulation Points.
- Click on the OK button to proceed.

Home Screen Process Flowchart
- Click on the Add menu in the Control bar.
- Select Add Composite.
The Composites dialog will open.
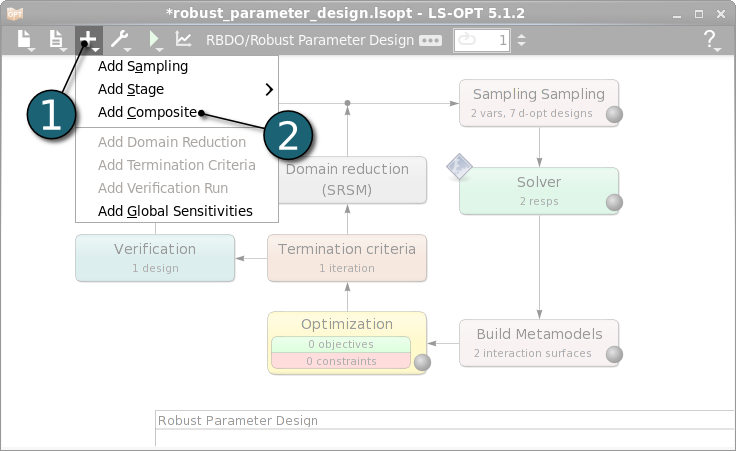
Define Composites
- Select Standard Deviation as a composite type.
- Enter std_stress as a Composite Name.
- Select the response Stress of which standard deviation is specified as the composite.
- Click on the OK button to end the definition of the composite expression.
- Click on the OK button to proceed.
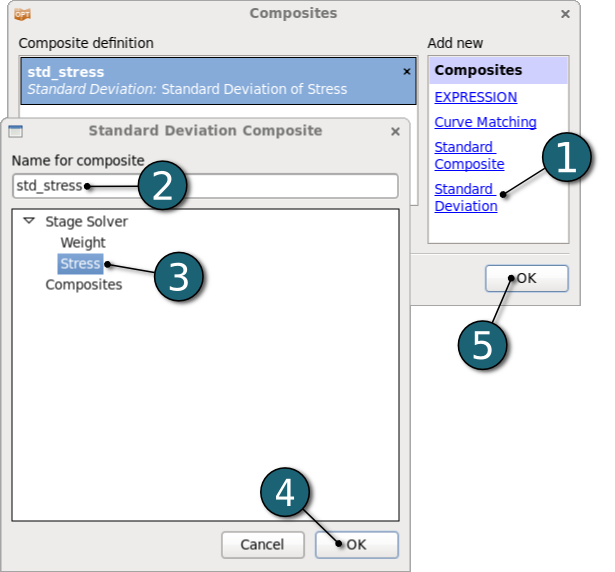
- After defining composite expression the Composite box takes its place in the Home Screen Process Flowchart.
Home Screen Process Flowchart
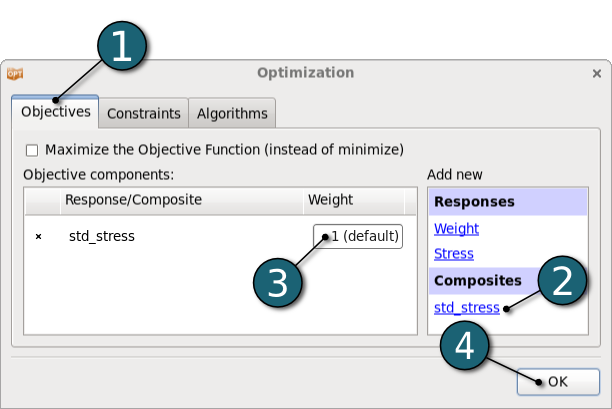
- Double click on the Optimization dialog to specify objectives and constraints for the design formulation and the optimization algorithm.
The Optimization dialog shall open.
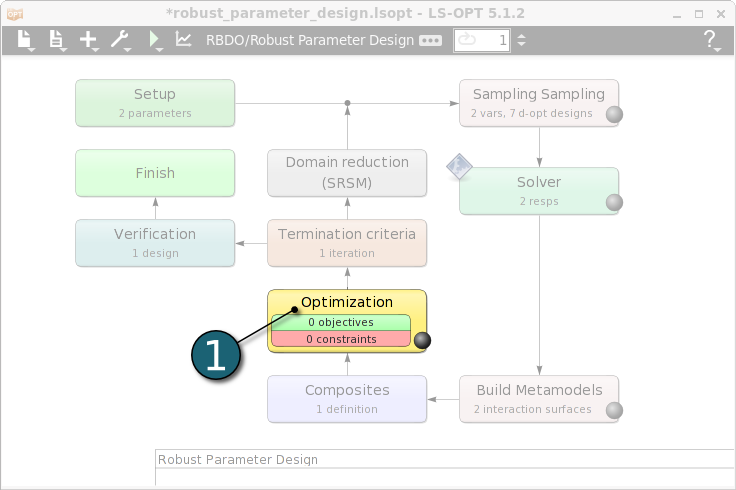
Define Objective
- Select the Objectives tab.
- From Composites list select std_stress as the objective.
- Use the default Weight 1. If you have multiple objectives, you may assign different weights to each one according to their importance.
- Click on the OK button to proceed.
Depending on the optimization task and strategy, the user can specify tolerances on the design change, the objective function change or the accuracy of the metamodel. The user can also specify whether termination is reached if any one, or all of these criteria are met.
Home Screen Process Flowchart
- Double click on the Termination criteria box.
A Termination Criteria window will open.
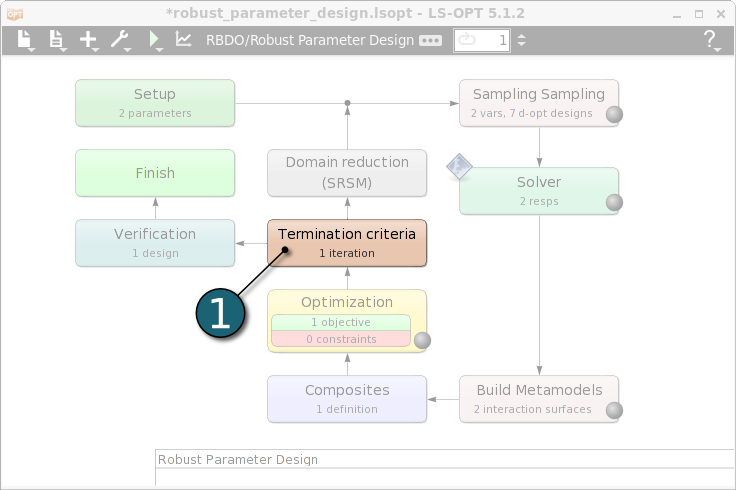
Define Termination Criteria
- Select Design AND Objective AND Metamodel Accuracy option for Tolerance Required for Termination.
- Use the default value 0.01 for the Design Change Tolerance.
- Use the default value 0.01 for the Objective Function Tolerance.
- Enter 10 for the Maximum number of iterations.
- Click on the OK button to proceed.
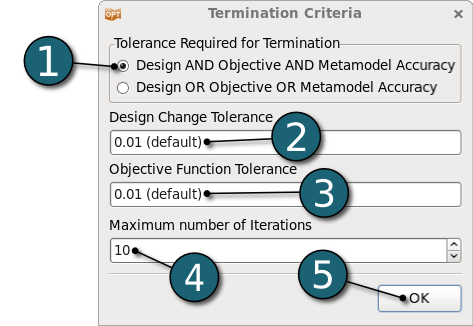
Home Screen Process Flowchart
Run LS-OPT
- Click on the Run button on the Control Bar.
- Click on the Normal Run.
- The user can get information on the status of the current iteration during execution.
- For every stage the user has the option to observe the progress of the program execution by selecting the LED at the corner on the Stage box. It is possible to observe the Progress and View Log for more information about the execution process.
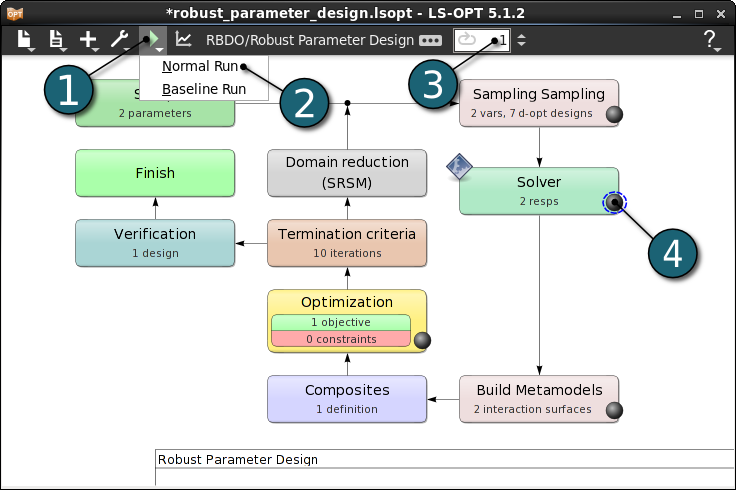
The optimization history of a variable, dependent, response, constraint, objective, multi-objective or the approximation error parameters of pure responses (not composites or expressions) shows the changes of the respective values of the optimum over the iterations.
Home Screen Process Flowchart
- Click on the Open the viewer icon in the control bar on the Home Screen Process Flowchart.
A New Plot window shall open.
- Choose History under the Optimization.

Optimization Histories
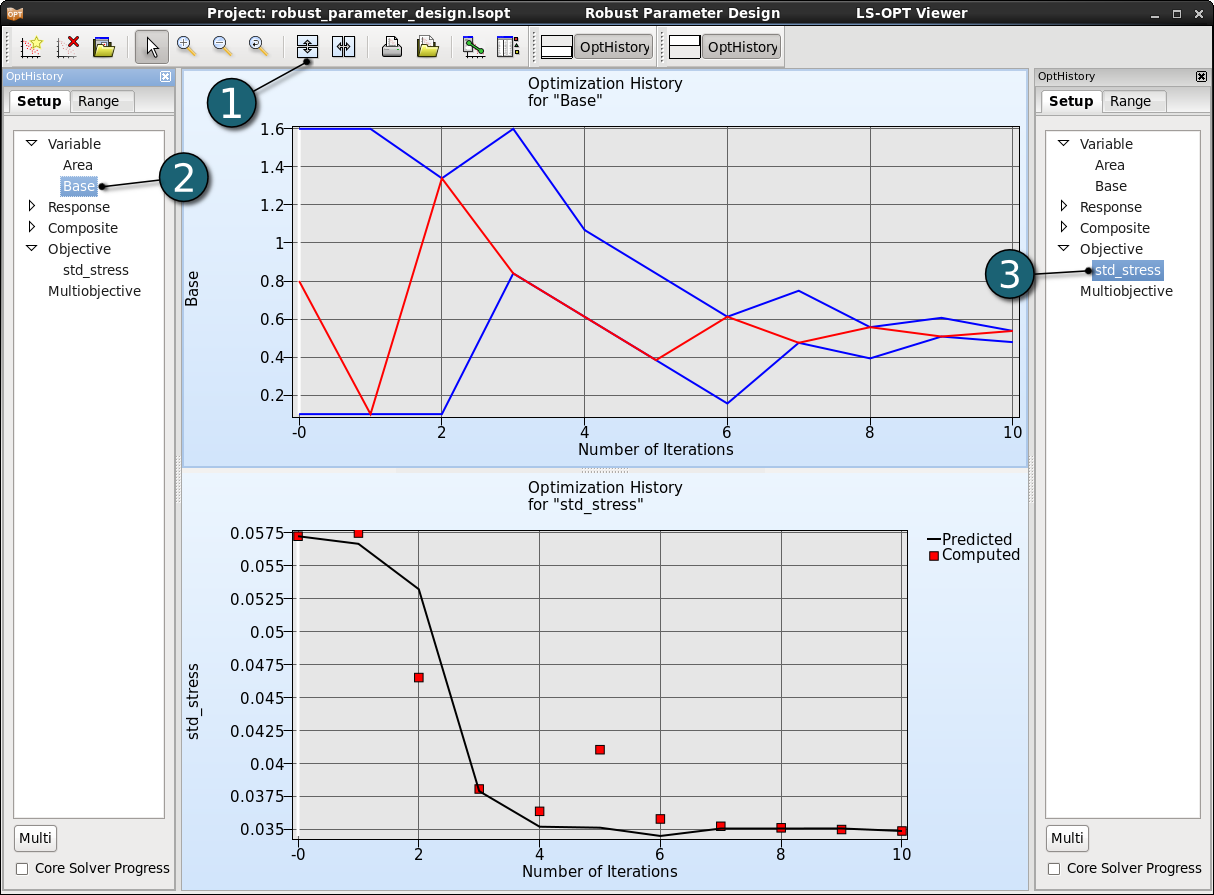
- Click on the Split vertical button to display two optimization histories together.
- Select variable Base in the Setup dialog of the first plot.
- Select objective std_stress in the Setup dialog of the second plot.
- For variables,the red line displays the variable value, and the blue lines the subregion bounds considered for the respective iteration.
- For responses and composites, the black solid line indicates the predicted values for the objective and constraint. The red squares represent the computed values of the optimal point of each iteration.
There is convergence of the variabe, and an improvement of the objecitve function.
New Plot - Statistical Tools
- Click on the New Plot icon in the menu bar - (or click on the Open the viewer icon on the Home Screen Process Flowchart).
A New Plot window shall open.
- Select Replace current plot icon.
- Select Statistical Tools under Stochastic analysis.
Histogram
- Select Setup tab in the new opened Statictical Tools plot window.
- Select the Plot type as Histogram.
- Select the response Stress to plot its histogram.
- Select Options tab.
- Select Frequency as Y-axis scaling.
- Display Mean Value, Standard deviation on the histogram.
- Display the histogram for the last iteration 10.
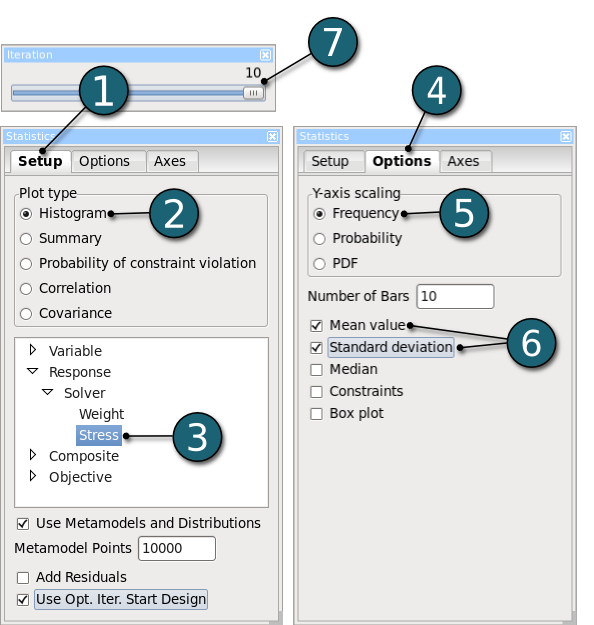
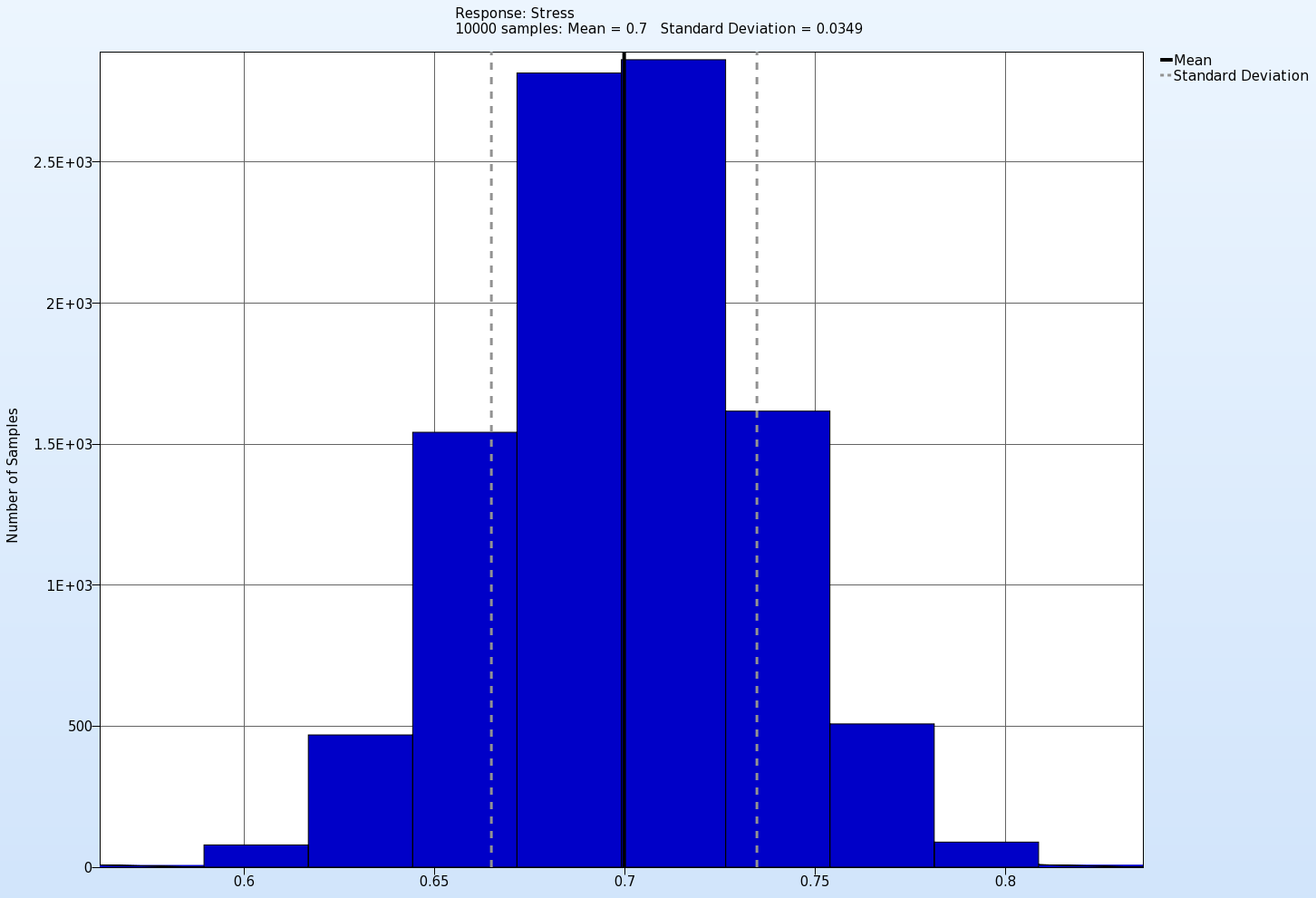
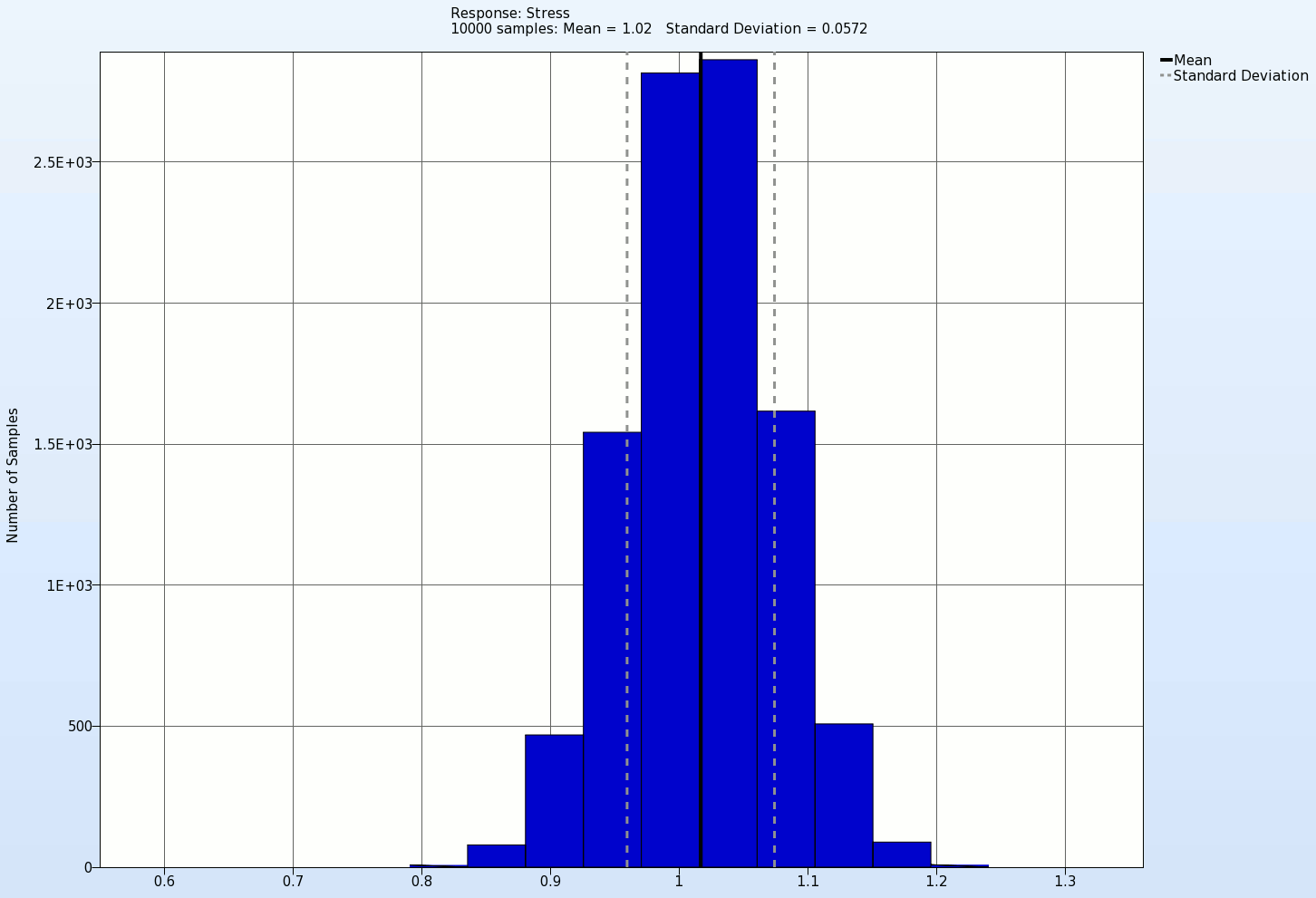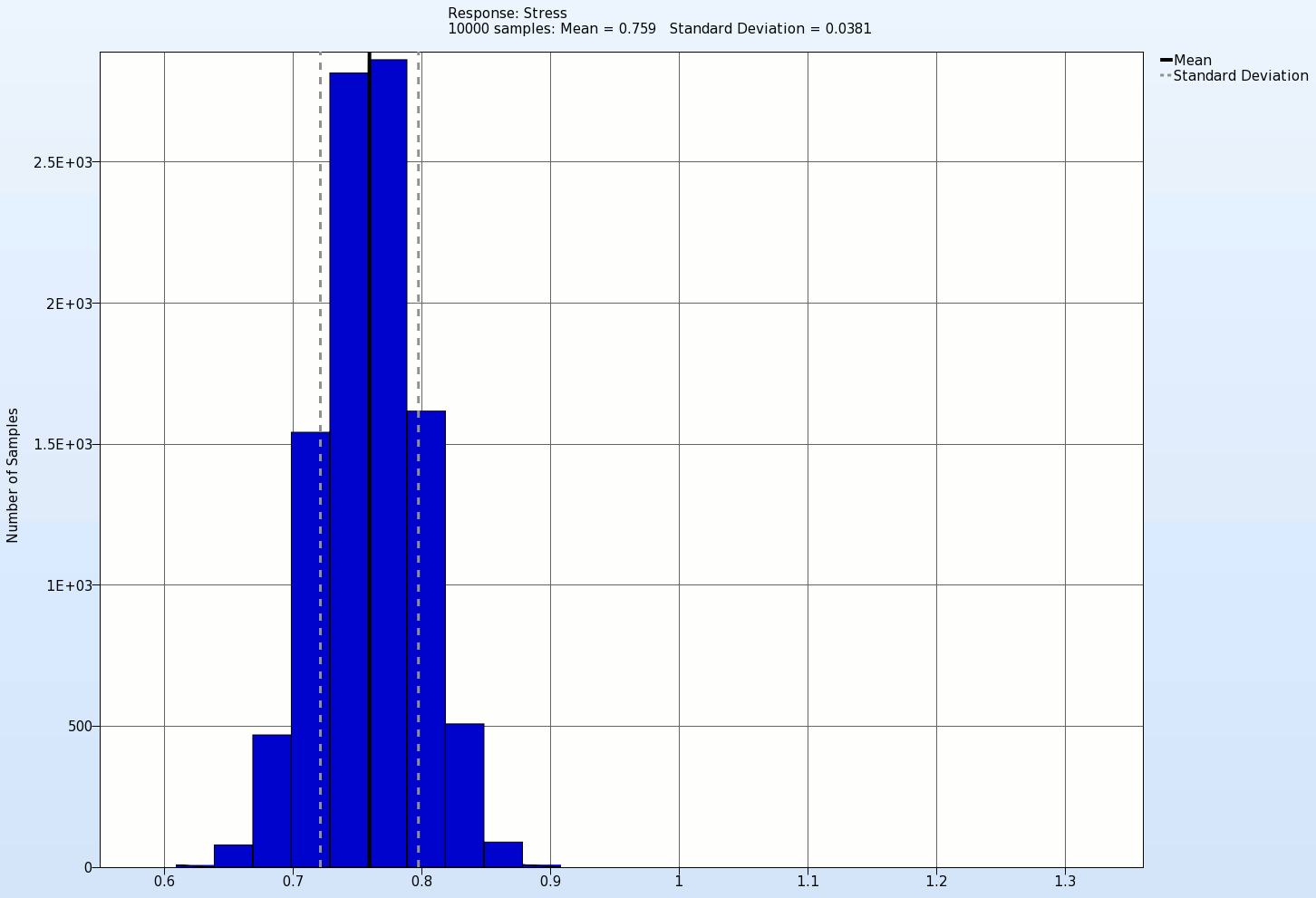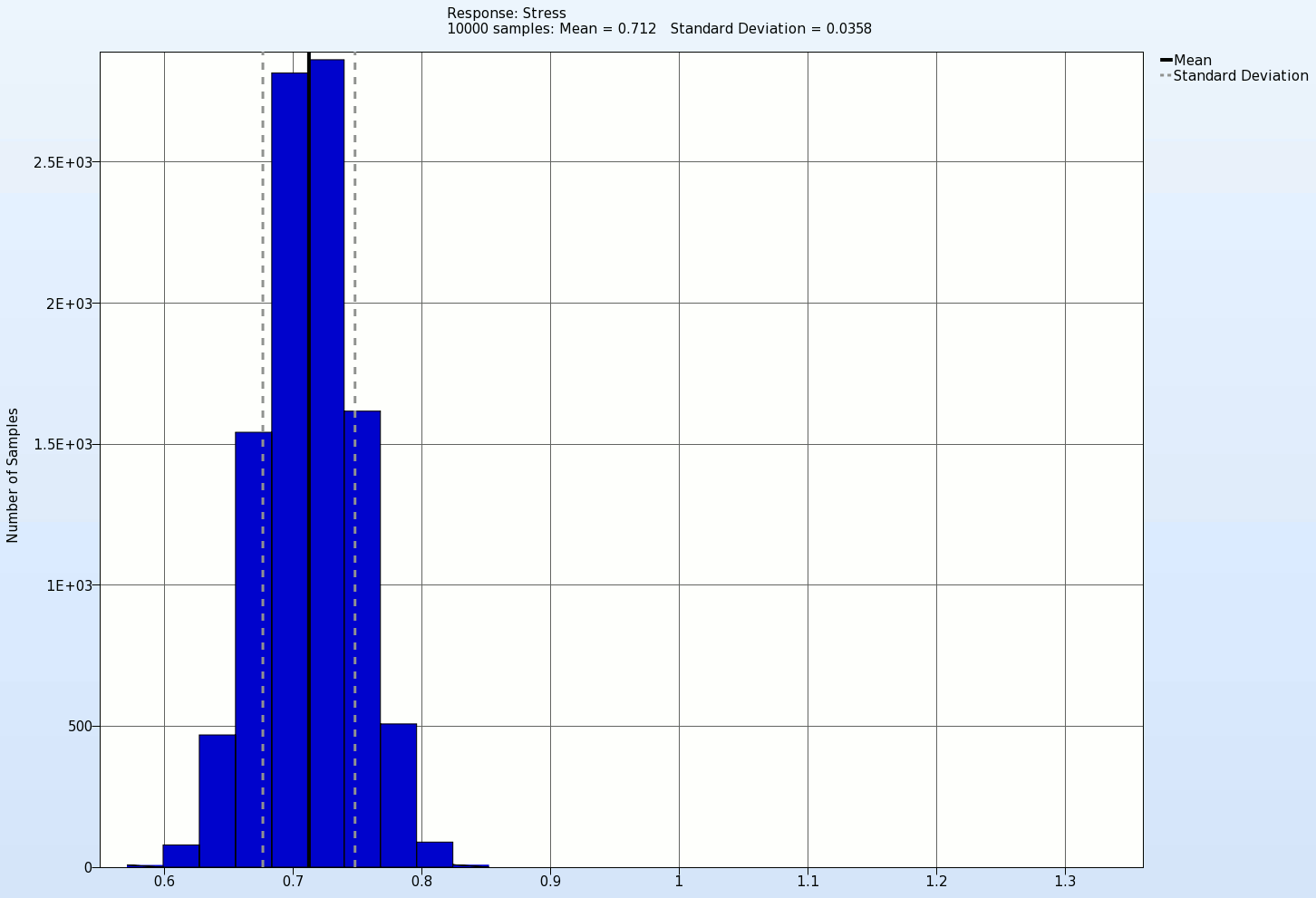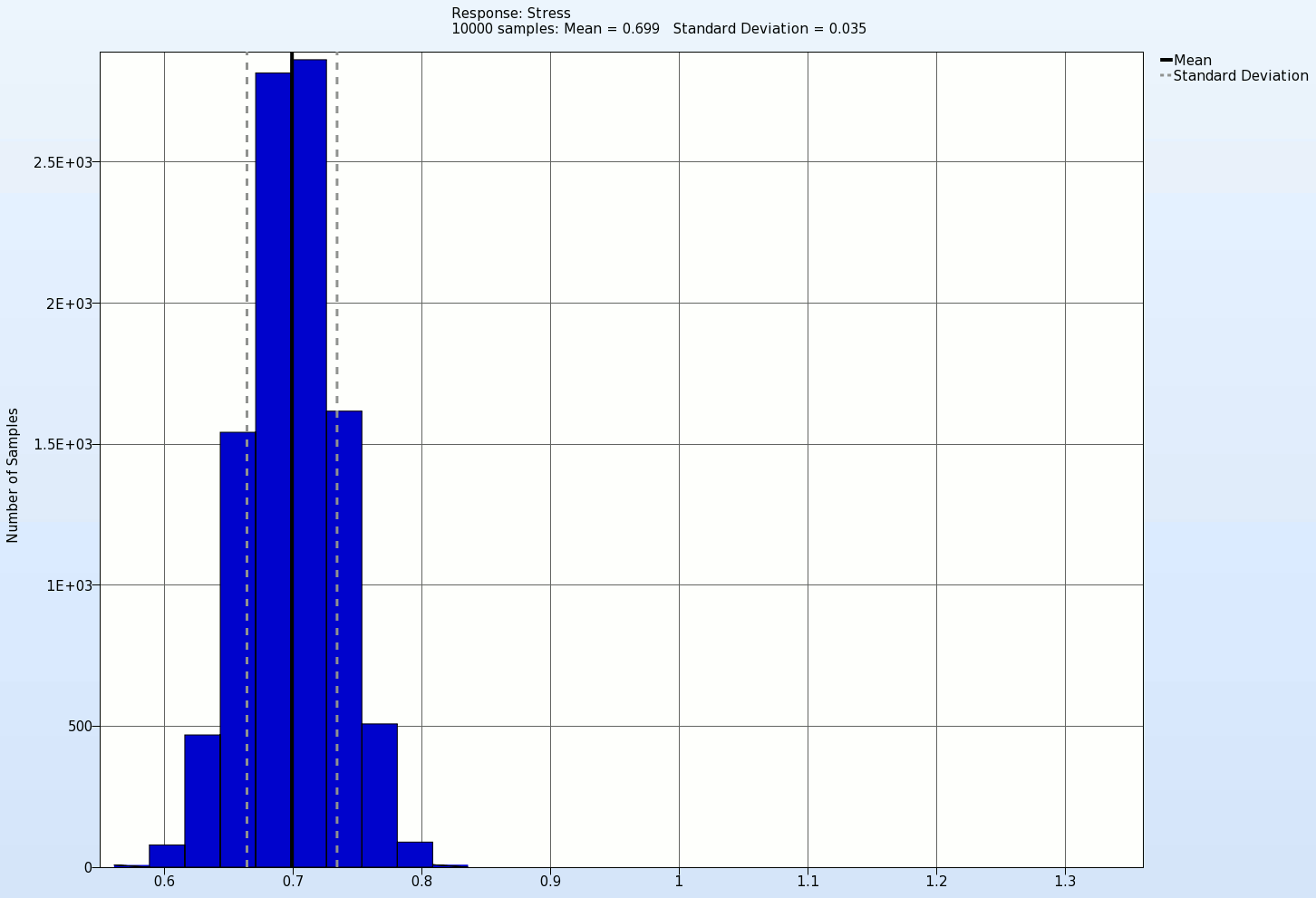
In the animation below the histogram of the response Stress with its mean and standard deviation values for each iteration is presented. Here we see that the Standard deviation of this response decreases with the increasing iteration number, which is actually the objective of this optimization problem.
For Linux : robust_parameter_design.tar.gz (1 kB)
For Windows : robust_parameter_design.zip (1.2 kB)
