Problem Description

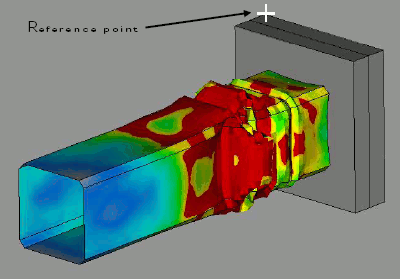
A front rail will be tested in crash simulation. The target is to find the best arrangement of its embosses in order to minimize the acceleration that appears in the test.

Constraints on the mass of the rail and the intrusion are specified.

• Objective function:
  • acceleration
• Constraints:
  • intrusion
  • mass

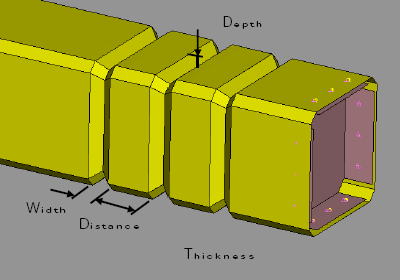
Design Variables

The design variables are:

• Depth of the embosses
  (-6 =< Emboss_depth  =< 0)
• Width of the embosses
  (-2 =< Emboss_width =< 2)
• Distance between embosses
  (-5 =< Emboss_dist =< 10)
• Thickness of rail
  (Thickness = {0.8, 0.9, 1.0, 1.1, 1.2, 1.4, 1.7})

Nominal Run

A first run of the nominal case (the rail without the embosses) can give an estimation of the values of acceleration, mass and intrusion.

All measurements took place at a reference point as shown at the picture on the right. Output results have been created for this position which are written in the d3thdt result file of LS-DYNA.

The values from the nominal run are:

• X acceleration  : -0.448 mm/s²
• X coordinate    : -314.8 mm
• Mass               : 1.6 Kg
• Barrier Mass    : 400.8 Kg
• Initial velocity   : 8 m/s
• Rail thickness  : 1.2 mm

The boundaries for the constraints are:

• Mass < 1.8
• X_coordinate < 241

Problem Solution

There are three steps needed to connect ANSA with LS-OPT:

• ANSA Morph (Model Definition)
  • morphing boxes
  • morphing parameters
  • parameters from ANSA Card entities
• ANSA Opt. Task (Task Manager Sequence Definition)
  • design variables for morphing parameters
  • design variables for ANSA parameters
  • session commands
  • design variables and FE output files
• LS-OPT setup
  • design variables
  • responses
  • objective function
  • constraints

Downloads

• ANSA_morph

• ANSA_opt_task

• RAIL